Lattice Boltzmann simulations of the dynamics of thin liquid films

Stefan Zitz

Defense, July 17th 2024, FAU & HI-ERN

thin film dynamics

\[\frac{\partial h(\mathbf{x},t)}{\partial t} = \nabla \cdot [M(h)\nabla p(\mathbf{x},t)] (+ X) \\ M(h) = \frac{h^3(\mathbf{x},t)}{3\mu}\quad \text{no-slip}\] Oron et al., Rev. Mod. Phys., 69 931 1997

Thin films interference

Thin-film interference, wikipedia.com

Printable OPV

T. R. Andersen et al., Energy Environ. Sci., 7 2014

Spreading, wetting & dewetting

Boltzmann equation

\[\partial_t f + \boldsymbol{\xi}\cdot\nabla f + \frac{\mathbf{F}}{\rho}\cdot\partial_{\boldsymbol{\xi}}f = \Omega(f) \] Evolution equation of a distribution function $f(\mathbf{x},\boldsymbol{\xi}, t)$ \[ [f] = \frac{kg~s^3}{m^6}\] T. Krüger et al., The Lattice Boltzmann Method: Principles and Practice, 2016

Moments

\[\rho(\mathbf{x}, t) = \int f(\mathbf{x},\boldsymbol{\xi}, t) \diff^3\xi \\ \rho\mathbf{u} = \int \boldsymbol{\xi}f(\mathbf{x},\boldsymbol{\xi}, t) \diff^3\xi \\ \rho E = \frac{1}{2}\int |\boldsymbol{\xi}|^2 f(\mathbf{x},\boldsymbol{\xi}, t) \diff^3\xi\]

\[\int \Omega(f) \diff^3\xi = 0 \\ \int \boldsymbol{\xi}\Omega(f) \diff^3\xi = \mathbf{0}\\ \int |\boldsymbol{\xi}|^2 \Omega(f) \diff^3\xi = 0\]

S. Succi, The Lattice Boltzmann Equation: For Fluid Dynamics and Beyond, 2001

The Collision operator

Dominated by two-body collisions of uncorrelated particles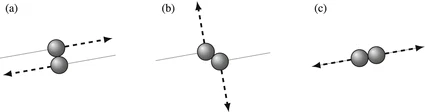

\[\Omega(f) = -\frac{1}{\tau} (f-f^{eq})\]

with $f^{eq}$ being a Maxwell-Boltzmann distribution

P.L. Bhatnagar, E.P. Gross, M. Krook, Phys. Rev., 93 (3) 1954

Hydrodynamic equations

\[\partial_t \int f \diff^3\xi + \int\boldsymbol{\xi}\cdot\nabla f \diff^3\xi + \frac{\mathbf{F}}{\rho}\cdot\int\partial_{\boldsymbol{\xi}}f \diff^3\xi \\= \int\Omega(f)\diff^3\xi \] \[ 0^{th}:\quad \partial_t\rho + \nabla\cdot(\rho\mathbf{u}) = 0\] \[ 1^{st}:\quad \partial_t(\rho\mathbf{u}) + \nabla\cdot(\rho\mathbf{u}\mathbf{u}) = \nabla\cdot\hat{\sigma} + \mathbf{F}\] S. Chen, G. D. Doolen, Annu. Rev. Fluid Mech., 30 (1) 1998

Chapman-Enskog

Stress tensor $\hat{\sigma}$ depends on $f$, but $f$ is unknowen \[f = f_{0} + \varepsilon f_1 + \varepsilon^2 f_2 + O(\varepsilon^3) \\ \partial_t = \varepsilon\partial_{t_1} + \varepsilon^2\partial_{t_2} + O(\varepsilon^3) \] with $f_0 \simeq f^{eq}$ and $\varepsilon \approx Kn$, at zeroth order
\[\partial_t(\rho\mathbf{u}) + \nabla\cdot(\rho\mathbf{u}\mathbf{u}) = -\nabla p + \mathbf{F}\ \] at first order we recover Navier-Stokes
S. Chapman, T. G. Cowling, 1990; D. Enskog, 1917

Swalbe.jl

Shallow WAter Lattice Boltzmann solvEr

\[\partial_t h + \nabla \cdot (h \mathbf{u}) = 0 \\ \partial_t (h \mathbf{u}) + \nabla \cdot (h \mathbf{u}\mathbf{u}) = -gh \nabla h +\\ \nu \nabla^2 (h\mathbf{u}) + 2\nu \nabla (\nabla \cdot (h\mathbf{u})) + \mathbf{F}_{tot}\]

W. Y. Tan, Shallow water hydrodynamics, 1992

Shallow water thin film?

Approximating thin films

\[ \mathbf{F}_{tot} = \mathbf{F}_{film} + \mathbf{F}_{fric} + \mathbf{F} \]

Quasisteady processes at low Re with subleading viscous terms

\[\partial_t h + \nabla \cdot (h \mathbf{u}) = 0 \\ 0 = -gh \nabla h - \frac{1}{\rho_0}h\nabla p - \nu\alpha_{\delta}(h) \mathbf{u} + \mathbf{F} \]

S. Zitz et al., Phys. Rev. E, 100(3) 2019

Swalbe.jl

“Weeks of coding have saved me hours of thinking.”

\[\partial_t h + \nabla \cdot (h \mathbf{u}) = 0\\ \mathbf{u} \approx \frac{1}{\nu \alpha(h)}\left(-gh \nabla h -\frac{1}{\rho_0}h\nabla p + \mathbf{F}\right) \\ \partial_t h \approx \nabla \cdot \left(\frac{h^3}{3\mu}\nabla p\right)\]

S. Zitz et al., JOSS, 7(77) 2022

dewetting

J. Becker et al., Nat. Mater., 2 2003

Thermal fluctuations

\[\partial_t h = \partial_x \left[\frac{h^3}{3\mu}\partial_x p + \sqrt{\frac{2k_BTh^3}{3\mu}}\mathcal{N}\right]\]

B. Davidovitch et al., PRL, 95 2005, G. Grün et al., J. Stat. Phys., 122 2006

Fluctuating thin films

\[ t_0 = \frac{3\mu}{\gamma h_0^3q_0^4} \] Length scale $2\pi/q_0$ \[ q_0^2 = \frac{1}{2\gamma}\frac{\partial \Pi(h)}{\partial h}\bigg\rvert_{h=h_0} \]

\[F_{\text{fluc}} = \rho_0^{-1}\sqrt{2 k_B T \mu \alpha_{\delta}(h)}\mathcal{N}\]

S. Zitz, A. Scagliarini, J. Harting, Phys. Rev. E, 104 2021

Rupture times

\[ \chi_{\sigma}(\theta) \sim \log\left(h_0 L^{1/2}/S_0^{1/2}\right)/\log\left(\frac{a \theta}{\sigma}\right) \propto \frac{1}{\log(\theta/\sigma)} \]

Fluctuation and pattern

\[ \Xi = \frac{\tau_d(\pi/6)}{\tau_d(\pi/9)} \propto {\frac{U(\pi/9)}{U(\pi/6)} \sim \frac{\left(\pi/9\right)^3}{\left(\pi/6\right)^3} = \left(\frac{2}{3}\right)^3 = 0.296...} \]

Fluctuation and sound

Switchable Substrates

\[\theta(\mathbf{x},t) = \theta_0 + \delta\theta\left[\sin(q_{\theta}(x+v_xt))\sin(q_{\theta}(y+v_yt))\right]\]

K. Ichimura et al., Science, 288, 2000

Static pattern

Zitz et al., Phys. Rev. Fluids, 8 2023

Droplet advection

Grawitter J., Stark H., Soft Matter, 17 2021

Three shades of dewetting

Morphologies

\[\Gamma = \frac{v_{\theta}}{U_{\theta}}, \quad U_{\theta} = \frac{\gamma\Theta^3}{9\mu}\]

Metastable rivulets

\[\Delta h(t)\sim \frac{\lambda}{v_{\theta}}e^{\alpha t},\quad \Delta h(\tau_{\text{riv}})\sim \beta h_0\\ \tau_{\text{riv}} \sim \log(v_{\theta})\sim\log(\Gamma)\]

Conclusion

“If the only tool you have is a hammer, it is tempting to treat everything as if it were a nail.”

Development of a LBM for thin liquid films
Effective solver for the stochastic thin film equation
Exciting dewetting state on switchable substrates

Thank you!